Antiparalelas

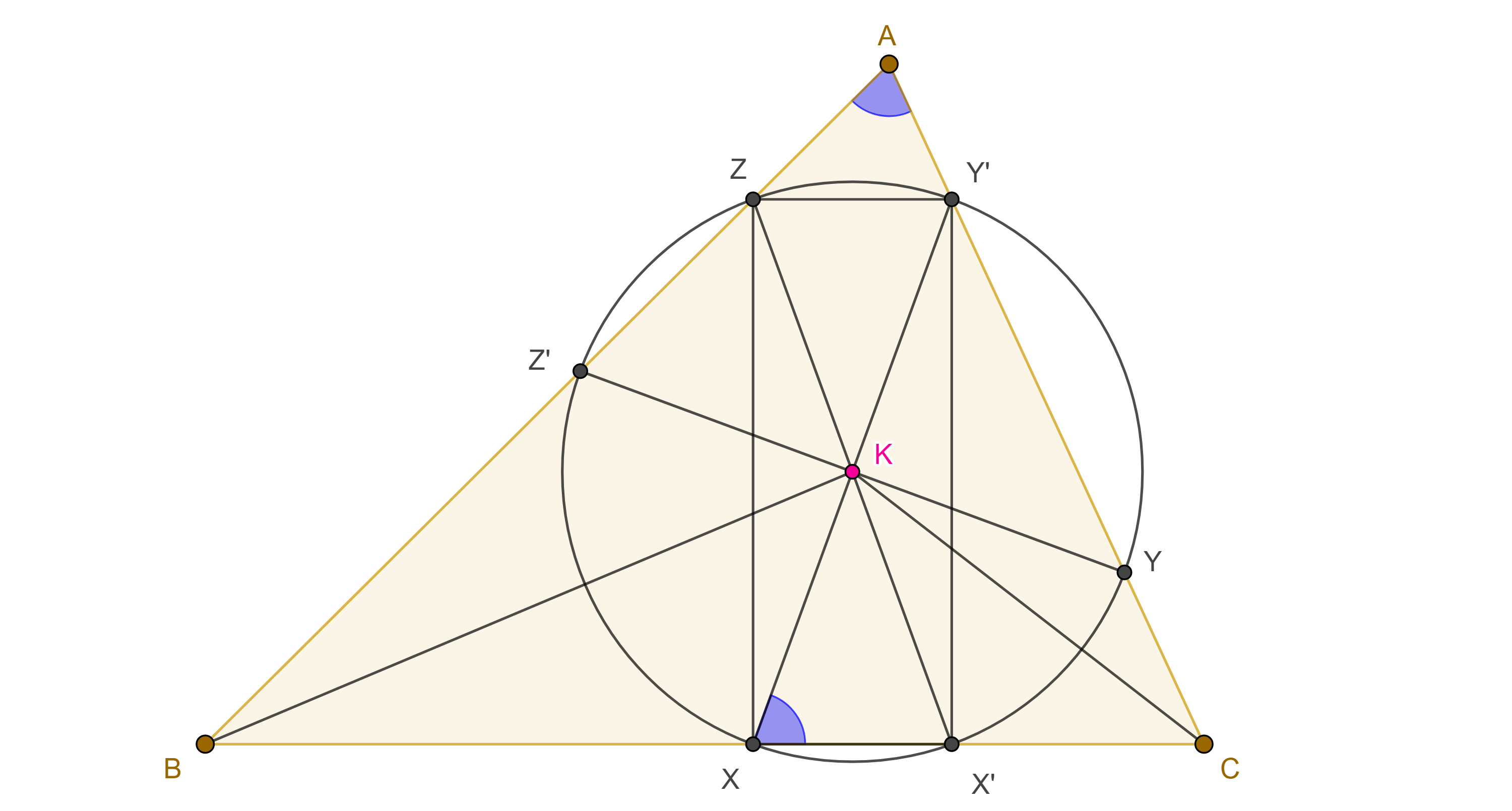
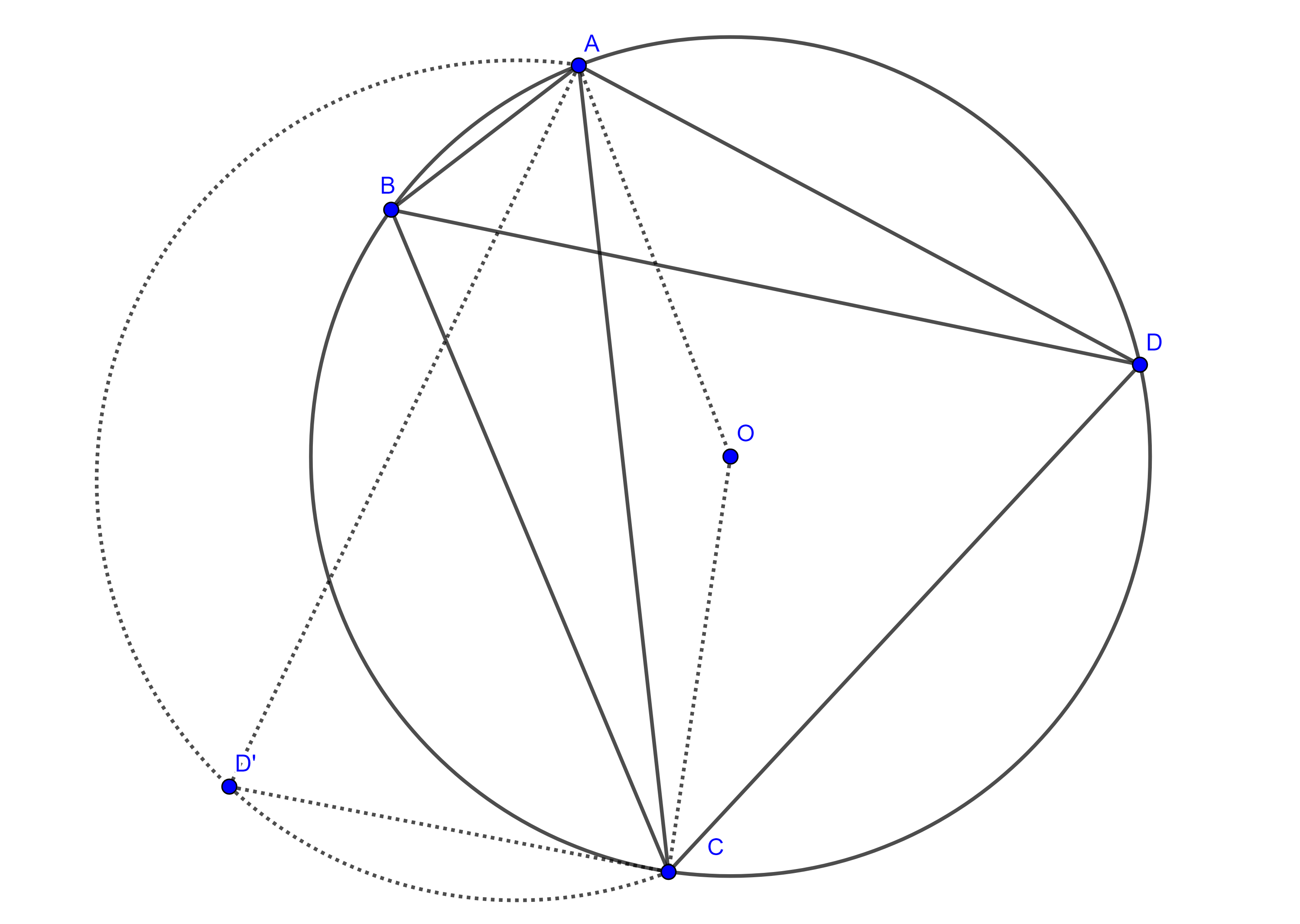
En geometría, un par de rectas concurrentes son antiparalelas una de la otra respecto a otro par de rectas si la bisectriz del ángulo que forma el primer par es perpendicular a la bisectriz del ángulo formado por las otras dos.

Sean las rectas ${\displaystyle r_{1},r_{2}}$ y otras dos ${\displaystyle s_{1},s_{2}}$ se dice que las primeras son antiparalelas a las segundas si las bisectrices de ${\displaystyle r_{1},r_{2}}$ son perpendiculares a las bisectrices de ${\displaystyle s_{1},s_{2}}$.^[1]​

Propiedades

• Si en uno de los pares de rectas antiparalelas se refleja una de ellas respecto a la bisectriz del otro par, el resultado es una recta paralela a la otra. Es esta propiedad la que da origen al nombre de antiparalelas.
• La propiedad de antiparalelismo es simétrica: si un par de rectas son antiparalelas respecto al segundo par, entonces el segundo par es antiparalelo respecto al primero.
• El cuadrilátero formado por las intersecciones de las rectas del primer par con el segundo siempre resulta en un cuadrilátero cíclico.
• Como hay cuatro rayos bisectrices para dos rectas concurrentes, para cada un de ellos se pueden trazar rectas antiparalelas.

Referencias

Obra consultable

• Levi S. Shively, Ph.D. (1961). «2». Introducción a la geometría moderna (Andrés Palacios Priego, trads.) [An Introduction To Modern Geometry]. Bolivia, Brasil, Costa Rica, Dominicana, Ecuador, El salvador, Estados Unidos, Guatemala, Honduras, Nicaragua, Panamá, Paraguay, Portugal, Puerto Rico, Uruguay: CIA. Editorial Continental, S. A. de C. V., Mexico. p. 24.