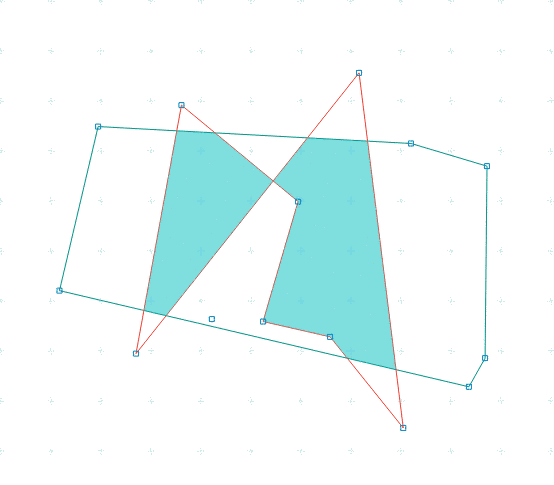
El algoritmo de Greiner-Hormann es utilizado en computación gráfica para recortar polígonos.[1] Es más eficiente que el algoritmo de Vatti, pero no puede gestionar eventuales casos degenerados.[2] Puede sin embargo utilizarse con polígonos que se auto-intersectan sin ser convexos. Puede fácilmente ser generalizado con el fin de efectuar otras operaciones booleanas sobre polígonos, tales que la unión y la diferencia.
El algoritmo está basado en la definición del "interior" de un polígono, ella misma basada en la noción de índice. Considera las regiones de índice par como interiores al polígono: esto es conocido también con el nombre de regla par-impar. El algoritmo toma dos listas de polígonos como entrada, cada polígono representado como una lista de cumbres conectadas.
En su formulación inicial, el algoritmo se divide en tres fases :
- En la primera fase, se calculan las intersecciones entre los lados de los polígonos. Las cumbres son añadidos a los puntos de intersección, y a cada uno se la agrega un apuntador hacia su homólogo del otro polígono.
- En la segunda fase, se marca cada intersección sea como una intersección de entrada, o como una intersección de salida. Esta decisión se toma aplicando la regla par-impar a la primera cumbre, después atravesando el polígono alternando las marcas (a una intersección de entrada tiene que seguir una intersección de salida).
- En la tercera y última fase, se genera el resultado. El algoritmo arranca de una intersección no tratada y escoge la dirección del recorrido del polígono, sobre la base de las marcas de entrada o salida: para una intersección de entrada, se atraviesa hacia adelante, y para una intersección de salida, atraviesa en sentido inverso. Se añaden las cumbres al resultado hasta que otra intersección sea encontrada; a continuación, el algoritmo se ocupa de la intersección correspondiente en el otro polígono y va a escoger nuevamente una dirección de recorrido, según la misma regla. Si la intersección siguiente ya ha sido tratada, el algoritmo se detiene para esta parte de la salida, y recomienza para las intersecciones no tratadas. La salida queda totalmente determinada cuando ya no quedan intersecciones sin tratar.
El algoritmo no se limita a los polígonos, y puede también bien tratar segmentos de curvas paramétricas.
Un de los inconvenientes mayores del algoritmo original es que no se ocupa de los casos degenerados, tales que las cumbres duplicadas o las auto-intersecciones tomando en cuenta una sola cumbre. La publicación original sugiere modificar ciertas cumbres para retirar los casos degenerados.
Véase también
- Algoritmo de Vatti
- Algoritmo de Sutherland-Hodgman
- Algoritmo de Weiler-Atherton
- Operaciones booleanas sobre polígonos
Referencias
Enlaces externos
- Geographic Clipping Describe los algoritmos de recorte usados en la librería D3.js.
- Implementación en Python y en Java.